Distribuição Exponencial: v.4.24
Distribuição Exponencial (ou exponencial negativa)
A distribuição exponencial pode ser associada com a distribuição geométrica. Porém antes de tratarmos das similaridades da propriedade dessas duas distribuições avaliaremos as características da variável aleatória.
De uma forma bastante resumida imagine uma variável aleatória Poisson, onde temos a contagem do número de ocorrências em um intervalo. Suponha agora que estejamos interessados em verificar a probabilidade do tempo transcorrido entre duas ocorrências consecutivas. Essa última é considerada uma variável aleatória exponencial.
Essa distribuição contínua que pode ser utilizada para descrever as probabilidades envolvidas no tempo que decorre para que um determinado evento aconteça. Existe uma conexão muito próxima entre a distribuição exponencial e a de Poisson. Ou seja, é Utilizada para descrever o tempo entre as ocorrências de sucessivos eventos de uma distribuição de Poisson.As relações entre as distribuições podem ser associadas a um processo estocástico, chamado de processo de poisson.
Para simplicar a abordagem imagine um processo de chegada sendo monitorando ao longo do tempo (sendo o tempo uma variável contínua).
Onde a taxa de chegada é um parâmetro associado λ por unidade de tempo.
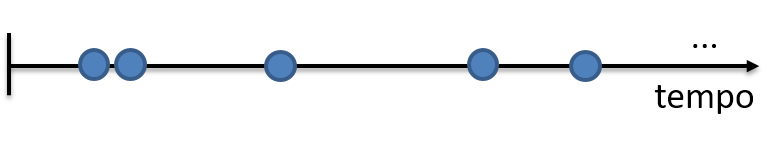
Para esse exemplo podemos estar interessados em algumas quantidades, como o número de chegadas em um determinado intervalo (contínuo). Essa quantidade é descrita por uma variável aleatória Poisson. Outra quantidade de interesse poderia ser a distribuição do tempo entre chegadas, onde essa quantidade é uma variável aleatória Exponencial.
Função Densidade de Probabilidade
f_X(x) = \lambda e^{-\lambda x} \quad 0 \le x < \infty
Sendo λ>0
Função de Distribuição Cumulativa
F_X(x)= \mathbb{P}(X \le x) = 1 - e^{-\lambda x} \quad x \ge 0
Sendo λ>0
Valor Esperado e Variância
E[X] = \frac{1}{\lambda} \\
V(X) = \frac{1}{\lambda^2}
Referência
Zibetti, Andre. Probabilidade. Distribuição Exponencial (ou exponencial negativa).
Como citar este texto:
Rodrigues, W.C., 2025. Distribuição Exponencial. DivEs - Diversidade de Espécies v.4.26.243.2508 (AntSoft Systems On Demand) - Guia do Usuário. Disponível em: <https://dives.antsoft.com.br>. Acesso em: 06/11/2025
Texto criado em: 07/04/2024 - Atualizado em: 07/04/2024
Versão do guia Online: 3.2.1.138.2505 - Atualizado em: 18/05/2025